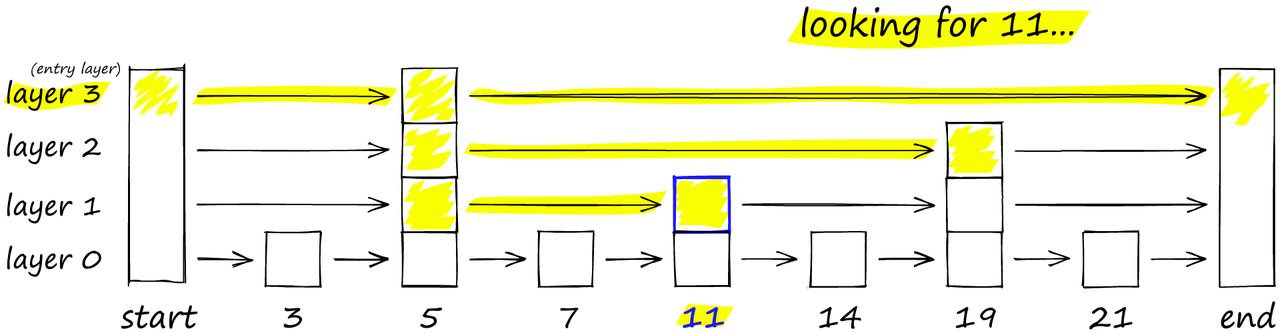
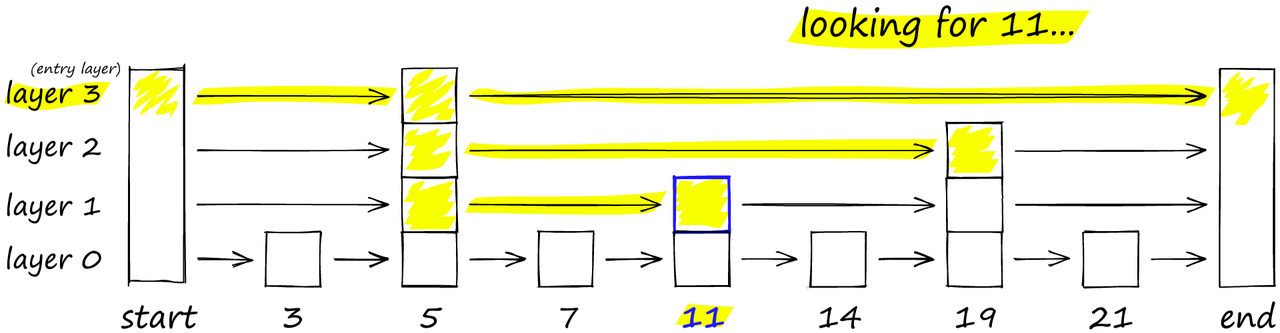
Aximof| 编辑

科技博文| 分类

HNSW，即Hierarchical Navigable Small World graphs（分层-可导航-小世界-图）的缩写，可以说是在工业界影响力最大的基于图的近似最近邻搜索算法（Approximate Nearest Neighbor，ANN），没有之一[1]。HNSW 是一种非常流行和强大的算法，具有超快的搜索速度和出色的召回率。

然而，尽管 HNSW 是一种用于ANN 的流行且稳健的算法，但要理解它的工作原理并不容易。

本文将帮助您解开 HNSW 的神秘面纱，并以易于理解的方式解释这个智能算法。在本文末尾，将介绍如何使用 Faiss 实现 HNSW，并选择适当的参数设置来实现所需的性能。

我们可以将 ANN 算法分为三个不同的类别：树、哈希和图。HNSW 属于图类别中的一种。更具体地说，它是一种接近图(proximity graph)，其中两个顶点根据它们的接近程度（越接近的顶点之间有链接）进行连接，近似距离通常以欧几里德距离来定义。

从 “proximity” 图到 “hierarchical navigable small world” 图之间存在着巨大的复杂性跳跃。我们将介绍两个最重要的技术，它们对 HNSW 算法有着很大的作用：概率跳表（the probability skip list）和可导航小世界图（navigable small world graphs）。

概率跳表最早由 William Pugh 于 1990 年提出 [2]。它可以像排序数组一样进行快速搜索，同时利用链表结构方便（且快速）地插入新元素（这是使用排序数组无法实现的）。

跳表通过构建多个链表层来工作。在第一层上，我们找到可以跳过多个中间节点 / 顶点的链接。随着我们向下移动到更低的层，每个链接跳过的节点数会减少。

要搜索跳表，我们从具有最长跳跃的最高层开始，沿着边向右移动（如下图所示）。如果我们发现当前节点的 “键” 大于我们要搜索的键，就说明我们超过了目标，因此我们向下移动到下一层中的前一个节点。例如，图中搜索‘11’时，先从最高层layer3开始向右移动，一直到end节点没有查询到目标值，所以返回到‘5’键值的节点并向下移动到layer2开始搜寻；当在layer2移动到‘19’键值的节点时，发现超过了目标，因此返回到前一节点的leyer1层开始寻找，直到最终搜索到‘11’.

在概率跳表结构中，我们从顶层开始。如果我们当前的键大于我们要搜索的键（或者到达了末尾），我们就跳到下一层。

HNSW 继承了相同的分层格式，最高层的边长最长（用于快速搜索），而较低层的边长较短（用于准确搜索）。

使用Navigable Small World（NSW）图进行向量搜索是在 2011-2014 年间的几篇论文中首次引入的 [4, 5, 6]。其想法是，如果我们构建一个接近图，使其既具有长距离链接又具有短距离链接，那么搜索时间将降低到(poly/）对数复杂度。

图中的每个顶点连接到其他几个顶点。我们将这些连接的顶点称为vertices friends，并且每个顶点都保留一个verticesfriends列表，从而创建了我们的图。

在搜索 NSW 图时，我们从预定义的入口点开始。这个入口点连接到附近的几个顶点。我们确定其中与我们的查询向量最接近的顶点，并移动到该顶点。

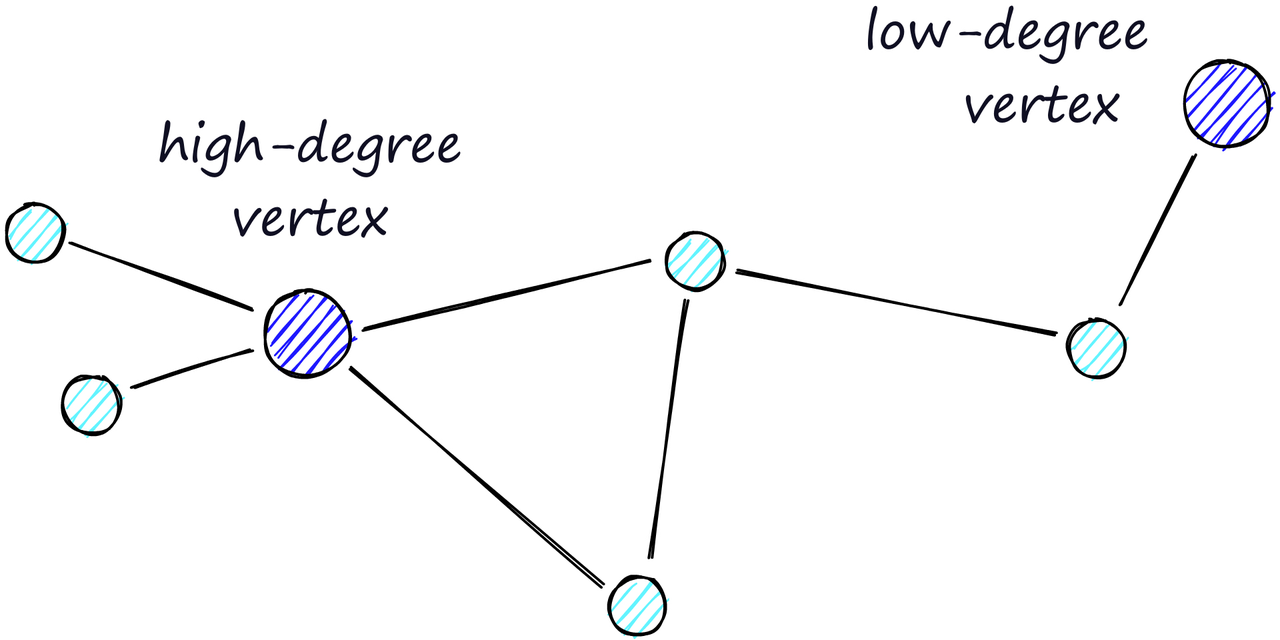
通过NSW图的搜索过程。从一个预定义的入口点开始，该算法贪婪地遍历到更接近查询向量的连接顶点

通过贪婪地遍历每个vertices friends列表中的最近邻顶点，我们重复执行greedy-routing搜索过程，从顶点移动到顶点。最终，我们将找不到比当前顶点更近的顶点 - 这是一个局部最小值，也是我们的停止条件。

使用贪婪路由的NSW模型被定义为具有（多项式 /）对数复杂度的任何网络。当图不可导航时（1-10K + 个顶点），贪婪路由的效率会降低 [7]。

路由（字面上是我们在图中采取的路径）由两个阶段组成。我们首先进行 “放大” （zoom-out”）阶段，在该阶段我们通过低度顶点（’度‘是一个顶点具有的链接数量）进行传递，然后进行 “缩小” 阶段，在该阶段我们通过高度顶点进行传递 [8]。

高度顶点具有许多链接，而低度顶点具有非常少的链接。

我们的停止条件是在当前顶点的vertices friends列表中找不到更近的顶点。由于这个原因，在放大阶段（较少的链接，更不可能找到更近的顶点）时，我们更有可能遇到局部最小值并过早停止。

为了最小化过早停止的概率（并增加召回率），我们可以增加顶点的平均度数，但这会增加网络的复杂性（和搜索时间）。因此，我们需要在召回率和搜索速度之间平衡顶点的平均度数。

另一种方法是从高度顶点开始搜索（首先进行缩小）。对于 NSW 来说，这确实提高了低维数据的性能。我们将看到这也是 HNSW 结构中的一个重要因素。

HNSW 是 NSW 的自然演化，它从 Pugh 的概率跳表结构中汲取了灵感，添加了层级的概念。

向 NSW 中添加层级会产生一个图，其中的链接在不同的层之间分离。在顶层，我们拥有最长的链接，在底层，我们拥有最短的链接。

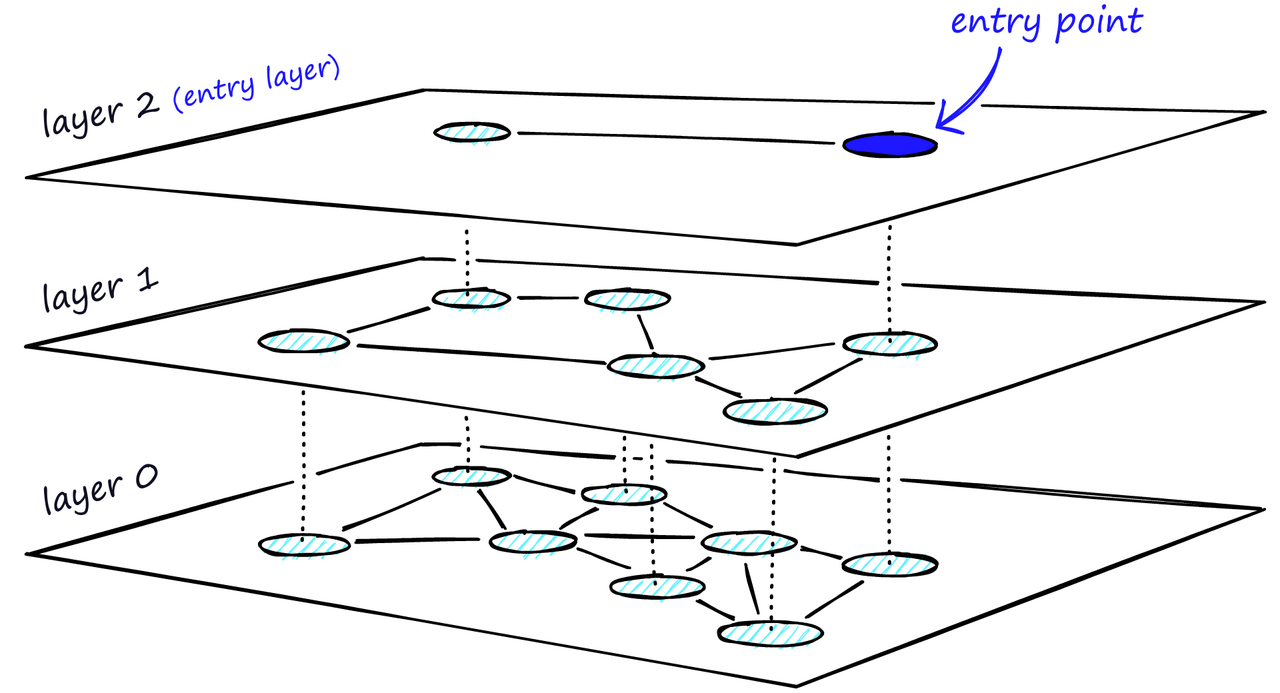
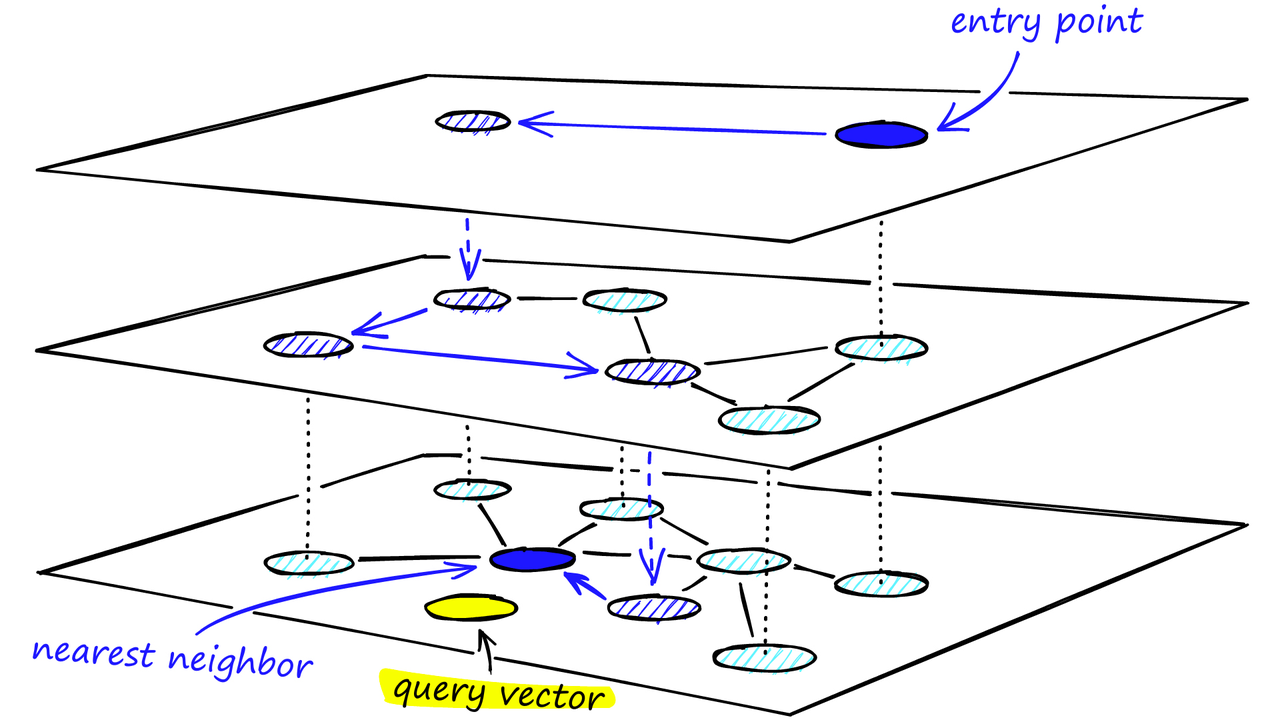
HNSW的分层图，顶层是我们的入口点，只包含最长的链接，随着我们往下移动，链接长度变得越来越短，越来越多。

在搜索过程中，我们进入顶层，找到最长的链接。这些顶点往往是高度顶点（具有在多个层之间分离的链接），这意味着我们默认情况下会从 NSW 中的缩小阶段开始。

我们沿着每个层的边缘遍历，就像我们在 NSW 中所做的那样，贪婪地移动到最近的顶点，直到找到一个局部最小值。与 NSW 不同的是，此时我们转移到较低层中的当前顶点，并开始再次搜索。我们重复这个过程，直到找到底层（层 0）的局部最小值。

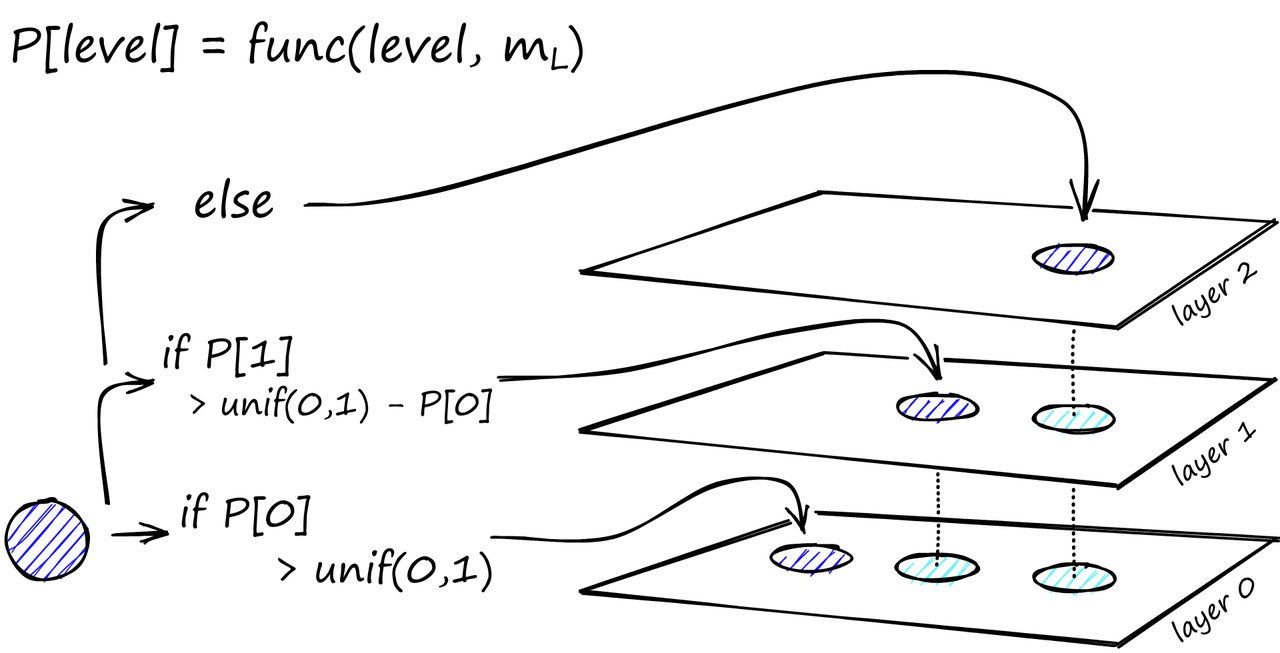
通过多层结构的HNSW图的搜索过程

在图构建过程中，向量逐个进行插入。层数由参数 L 表示。向量在给定层插入的概率由一个由*‘level multiplier’ m_L归一化的概率函数给出，其中m_L = ~0*表示向量仅在第0层插入。

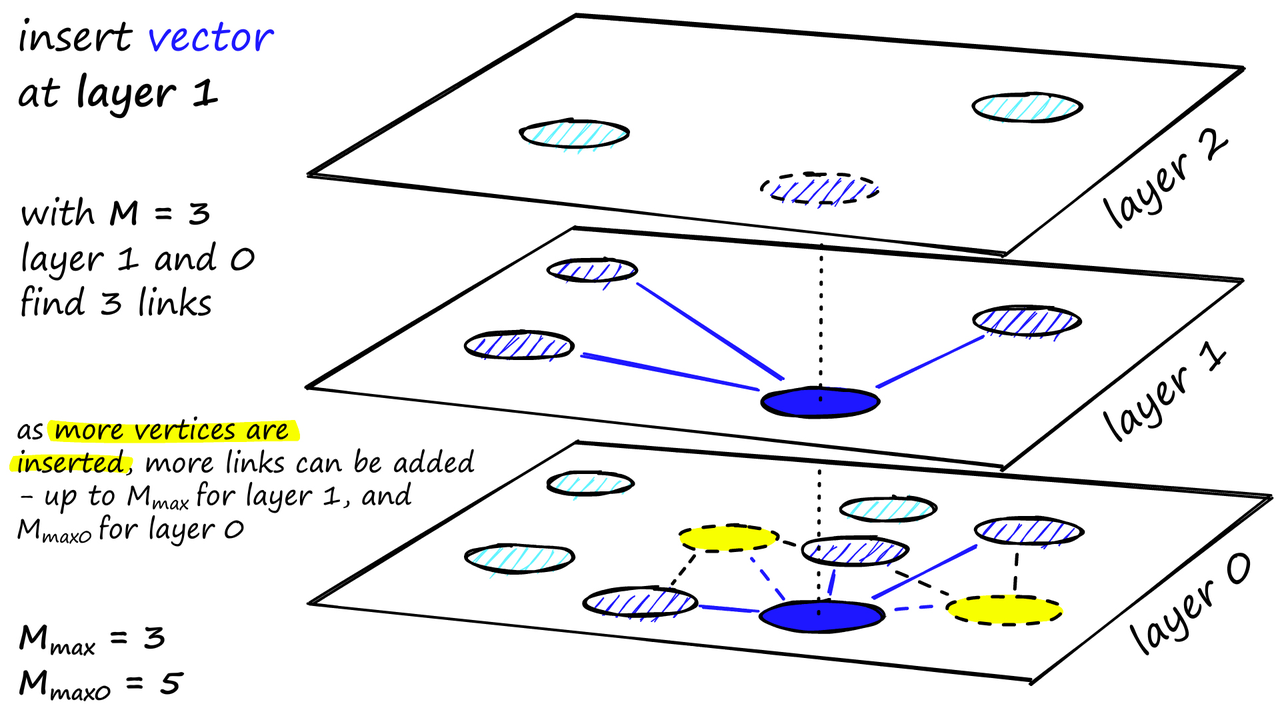
对于每个层（除了层 0），概率函数都会重复一次。将向量添加到其插入层以及下面的每一层。

HNSW 的构建发现，当我们最小化跨层共享邻居的重叠时，可以获得最佳性能。减小 m_L 可以帮助减少重叠（将更多向量推到层 0），但这会增加搜索过程中的平均遍历次数。因此，我们使用平衡两者的 m_L 值。这个最优值的经验法则是 1/ln (M)[1]。

图构建从顶层开始。在进入图之后，算法会贪婪地沿着边缘遍历，找到与我们插入的向量 q 最近的 ef个最近邻顶点 - 此时 ef = 1。

在找到局部最小值之后，它转移到下一层（与搜索过程中所做的一样）。重复这个过程，直到到达我们选择的插入层。这里开始了第二阶段的构建。

ef 值增加到 efConstruction（我们设置的参数），意味着将返回更多的最近邻顶点。在第二阶段，这些最近邻顶点成为与新插入的元素 q 的链接的候选顶点，也是下一层的入口点。

从这些候选顶点中选择 M 个邻居作为链接 - 最简单的选择标准是选择最接近的向量。

经过多次迭代之后，当添加链接时，还会考虑两个参数：M_max（定义一个顶点可以拥有的最大链接数）和 M_max0（定义层 0 中的顶点具有的最大链接数）。

分配给每个顶点的链接数以及M、M_max和M_max0的效果

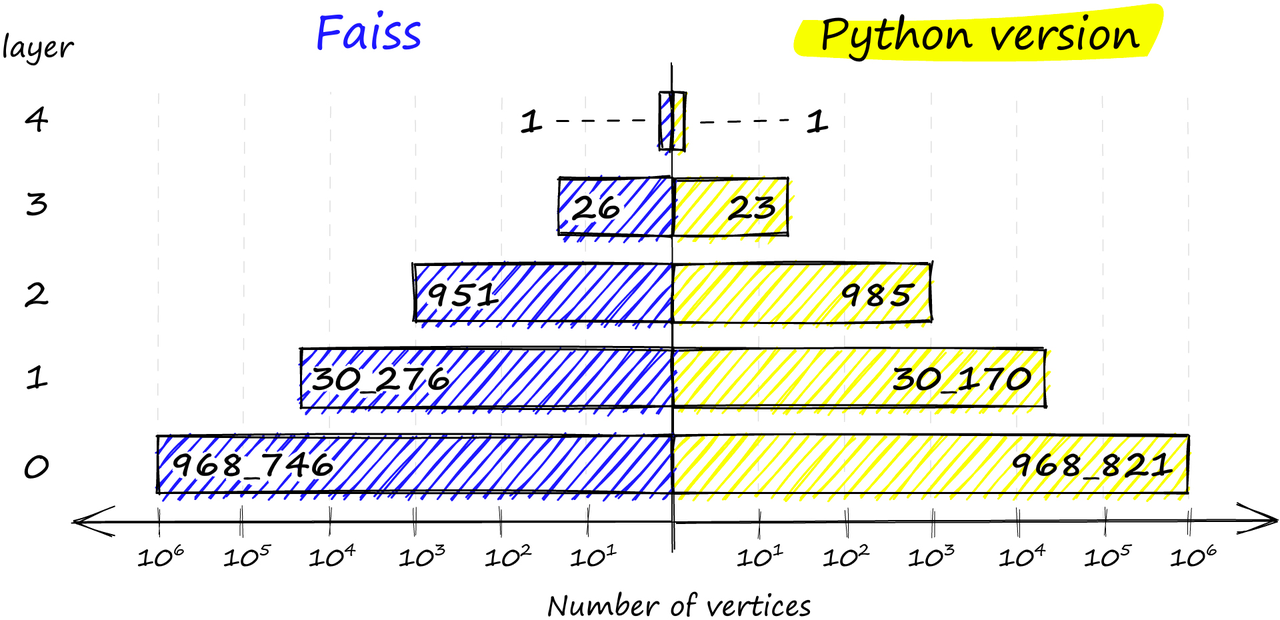
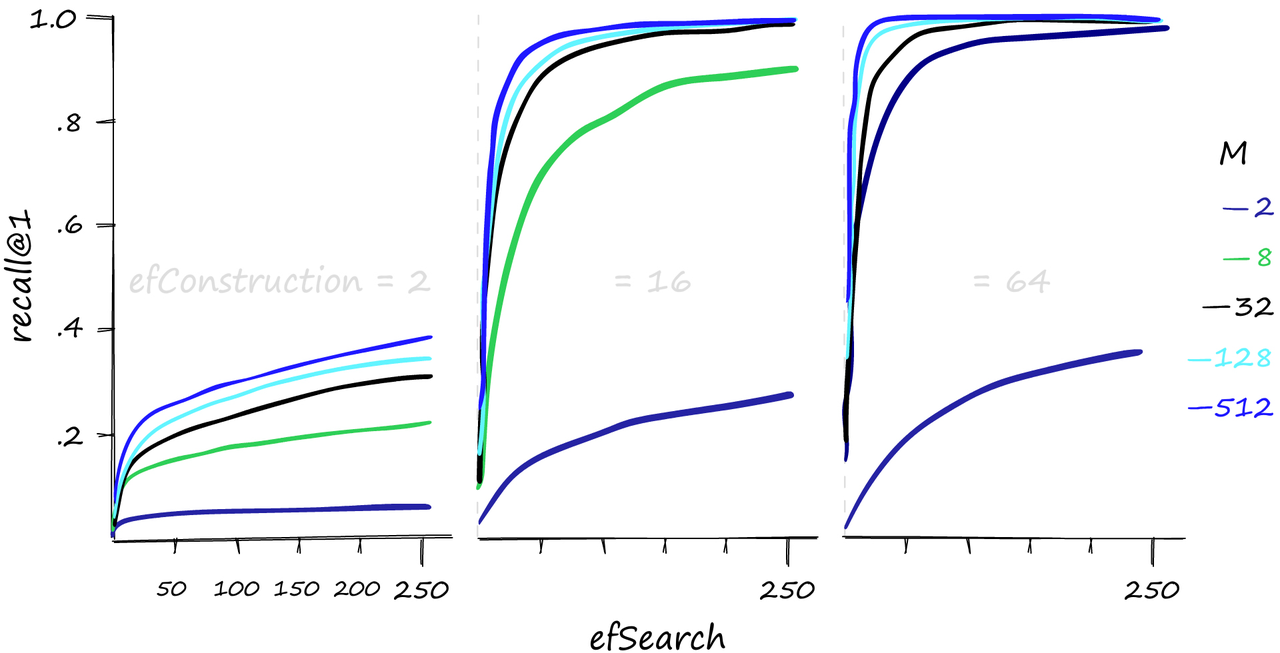
插入的停止条件是在层 0 中找到局部最小值。

我们将使用 *Facebook AI Similarity Search（Faiss）*库实现 HNSW，并测试不同的构建和搜索参数，以查看它们如何影响索引的性能。

要初始化 HNSW 索引，我们编写以下代码：

这样，我们就设置了 M 参数 - 每个顶点添加的邻居数，但我们还缺少 M_max 和 M_max0。

在 Faiss 中，这两个参数是在索引初始化时自动设置的 set_default_probas 方法中调用的。M_max 值设置为 M，M_max0 设置为 M2*。

在使用*index.add (xb)*构建索引之前，我们将发现层数（或 Faiss 中的级别）未设置：

-1

array([], dtype=int64)

如果我们继续构建索引，在构建之前这两个参数需要设置：

开始图的构建，xb为(1000000, 128)数据，构建需要一点时间；

4

这里我们有图中的level数，0->4，如 max_level 所述。

array([ 0, 968746, 30276, 951, 26, 1], dtype=int64)

并且有 levels，它显示了从 0 到 4 每个级别上的顶点的分布（忽略第一个 0 值）。我们甚至可以找到哪个向量是我们的入口点：

118295

这是我们使用 Faiss 实现的 HNSW 图的高级视图，但在测试索引之前，让我们深入了解 Faiss 是如何构建这个结构的。

当我们初始化索引时，我们传递了向量的维度 d 和每个顶点的邻居数 M。这会调用 “set_default_probas” 方法，传递 M和*1 /log (M)*作为 levelMult（相当于上面的 m_L）的位置参数。该方法的 Python 等效代码如下：

在这里，会产生两个向量,分别是 - assign_probas，表示在给定层插入的概率，cum_nneighbor_per_level，表示在不同的插入级别上分配给顶点的最近邻的累积总数。

([0.96875, 0.030273437499999986, 0.0009460449218749991, 2.956390380859371e-05, 9.23871994018553e-07, 2.887099981307982e-08], [64, 96, 128, 160, 192, 224])

通过这个函数，我们可以看到在级别 0 上插入向量的概率要比更高的级别高得多（尽管，如下面所解释的那样，概率并不完全如此定义）。这个函数意味着更高的级别更稀疏，减少了 “被困住” 的可能性，并确保我们从更长的范围遍历开始。

我们的 assign_probas 向量被另一个名为 random_level 的方法使用 - 在这个函数中，每个顶点被分配一个插入级别。

我们使用 NumPy 的随机数生成器 rng（以下面初始化为例）生成一个随机浮点数 f。对于每个level，我们检查 f 是否小于 assign_probas 中为该level分配的概率 - 如果是，那就是我们的插入层。

如果 f 太高，我们从 f 中减去 assign_probas 值，并在下一个level上重试。这个情况的结果是，向量最有可能插入级别 0，但如果不是，则插入的概率在逐级增加。

最后，如果没有level满足概率条件，我们在最高级别插入向量，即返回 len (assign_probas) - 1。

array([968821, 30170, 985, 23, 1], dtype=int64)

如果我们比较 Python 实现和 Faiss 实现之间的分布，我们会发现非常相似的分布结果：

Faiss实现(左)和Python实现(右)中跨层的顶点分布

Faiss 实现还确保我们始终在最高层中有至少一个顶点，作为我们图的入口点。

我们需要大量的向量才能将它们分配到顶层5 -(如使用的1_000_000样本大小)，实际上不会在这个更高的层返回任何顶点，实际上只在第4层返回一个顶点。

可以通过减少或增加level multiplier m_L来增加在更高层插入的可能性，但差异很小，非常随机(概率可能向上/向下移动)，并且还会改变计算出的最佳层数，因此除非您有特定的原因，否则不值得更改-并且Faiss不支持更改这一点(至少从Python包装器中)。我们可以像下面看到的那样访问set_default_probas函数，但是在修改值时不会看到任何影响。

首先让我们看看使用Python实现的当前值和期望值是什么，当使用M == 32时，Faiss将把m_L设置为1/log(M)，这使我们得到0.2885:

0.28853900817779266

使用Python实现输出更改M和m_L参数:

([0.9999850546614752, 1.4945115161637832e-05], [64, 96])

在 Faiss 中，我们可以使用 ‘default’ 执行查看每个level的分布。

array([ 0, 968746, 30276, 951, 26, 1], dtype=int64)

最后，让我们验证m_L值~0产生单层HNSW图(例如NSW图):

([1.0], [64])

Faiss还总是确保至少有一个顶点包含在最高级别，比如我们构建一个小数据量的索引:

array([ 0, 974, 25, 1], dtype=int64)

既然我们已经探索了HNSW背后的理论以及它在Faiss中是如何实现的——让我们看看不同参数对我们的调用、搜索和构建时间的影响，以及它们的内存使用情况。

我们将修改三个参数:M、efSearch和efConstruction。在本案例中我们将索引Sift1M数据集.

另外两个参数，efConstruction和efSearch可以在我们初始化索引之后修改。

我们的efConstruction值必须在我们通过index.add(xb)构造索引之前设置，但是efSearch值可以在搜索之前随时设置。 先来看看召回性能；

各种M, efConstruction和efSearch参数的Recall@1性能。

较高的M和efSearch值会对召回性能产生很大的影响——而且很明显，需要一个合理的efConstruction值。我们还可以增加efConstruction以在较低的M和efSearch值下获得更高的召回率。

然而，这种性能并不是白来的。通常情况下，我们需要在召回和搜索时间之间有一个平衡。

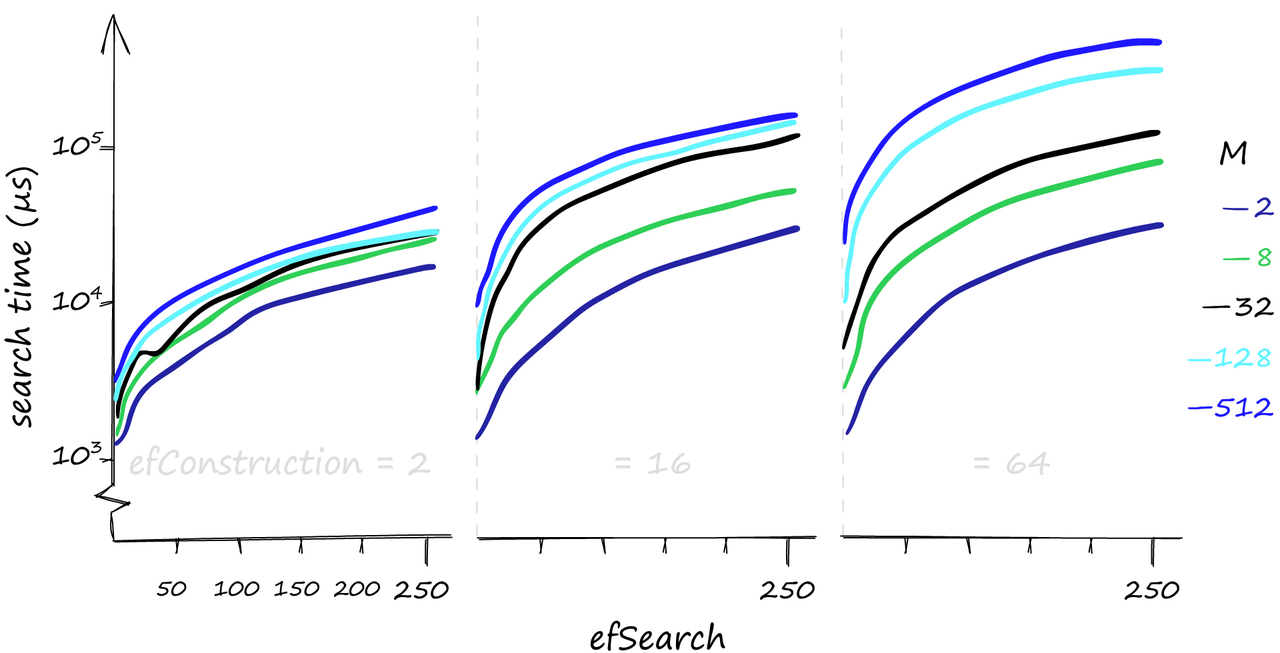
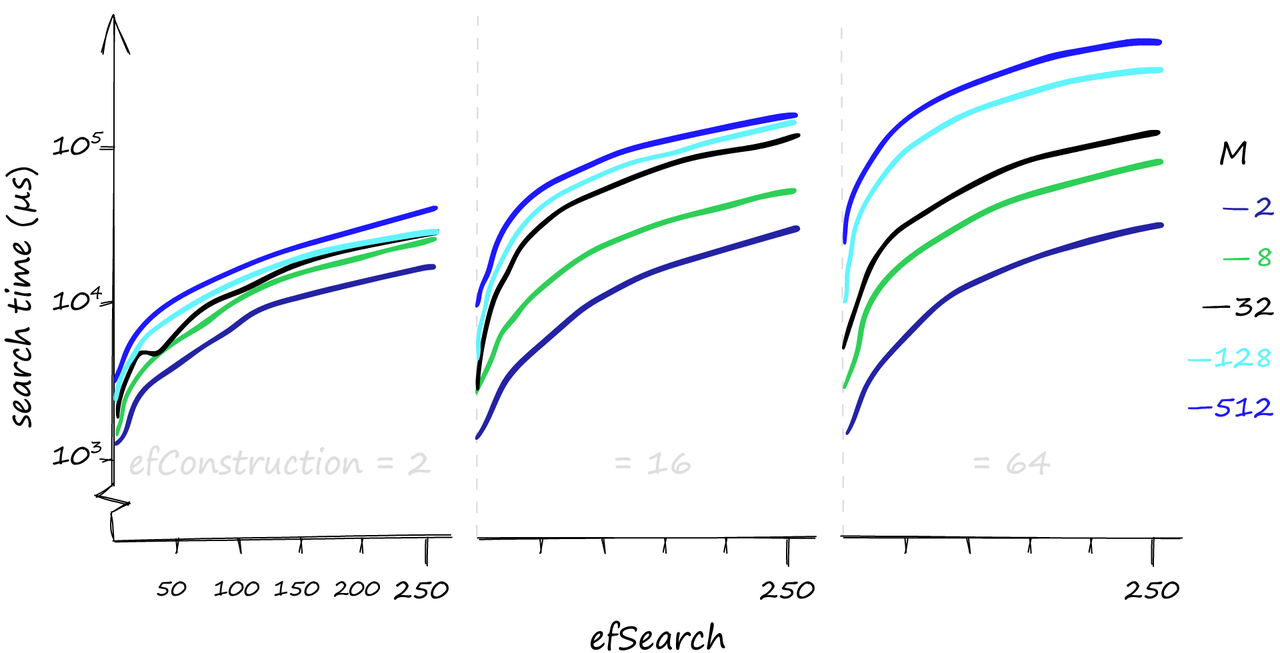
当搜索1000个查询时，各种M, efConstruction和efSearch参数的搜索时间,以µs为单位。（y轴使用对数刻度）

虽然较高的参数值可以提供更好的召回，但对搜索时间的影响可能是巨大的。这里我们搜索1000个相似的向量(xq[:1000])，我们的召回/搜索时间可以从80%-1ms到100%-50ms不等。如果我们对一个相当糟糕的召回率感到满意，搜索时间甚至可以达到0.1毫秒。

当我们使用少量查询进行搜索时，efConstruction确实对搜索时间影响很小。但是对于这里使用的1000个查询，efConstruction的影响变得非常重要。

如果您认为您的查询将主要是低容量的，那么增加efConstruction是一个很好的方式。它可以在不影响搜索时间的情况下提高召回率，特别是在使用较低的M值时。

只搜索一个查询时的构造和搜索时间;当使用较低的M值时，对于不同的efConstruction值，搜索时间几乎保持不变

这些看起来都很棒，但是HNSW索引的内存使用情况如何呢?然而在这块，事情可能会变得不那么吸引人。

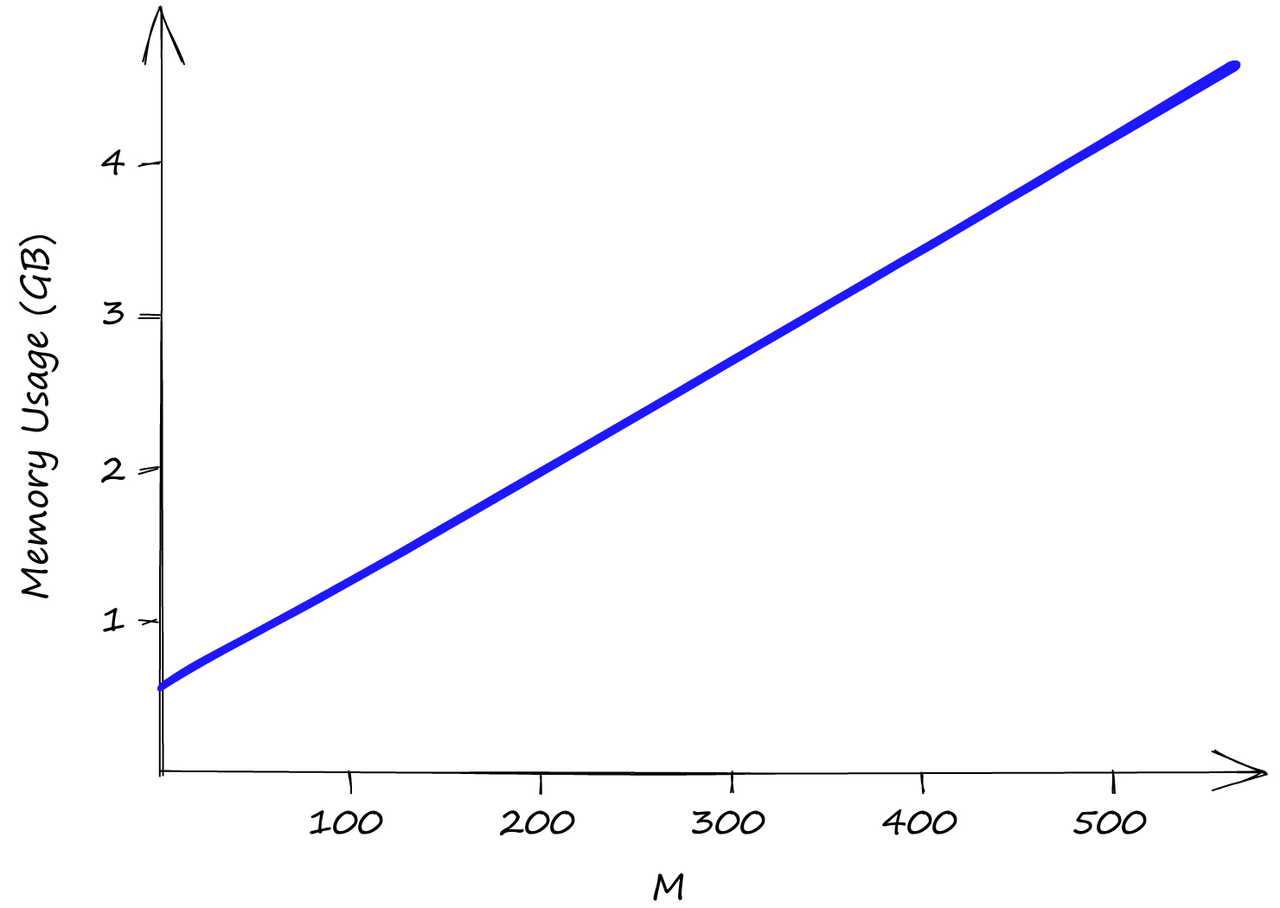
使用我们的Sift1M数据集，随着M值的增加，内存使用情况。efSearch和efConstruction对内存使用没有影响.

efConstruction和efSearch都不影响索引内存的使用，那只有M。即使M是低值2，我们的索引大小也已经超过了0.5GB，当M为512时，索引大小几乎达到了5GB。

因此，尽管HNSW产生了令人难以置信的性能，但我们需要将其与高内存使用量和由此产生的不可避免的高基础设施成本进行权衡。

就内存利用率而言，HNSW不是最好的索引。但是，如果必需要用到HNSW时，我们可以通过使用积量化(PQ)压缩向量来改进它。使用PQ将减少召回并增加搜索时间——但通常，ANN的大部分都是在平衡这三个因素。

如果，相反我们想提高我们的搜索速度-我们也可以这样做。我们所做的就是在我们的Index中加入IVF(倒排索引) 的成分。当然将IVF或PQ添加到我们的索引中有很多需要讨论的问题。

这篇文章的内容就到这里了，HNSW 算法是一种用于向量相似性搜索的算法。它是基于可导航小世界图的概念，在构建图结构时具有高效的性能。HNSW 算法的实现可以提高搜索速度，但会增加内存使用。可以通过使用积量化 (PQ) 压缩向量来改进内存利用率。另外，将倒排索引 (IVF) 或 PQ 添加到索引中也可以提高搜索速度。需要根据具体应用场景来选择适合的优化方法。